Формулы сокращенного умножения (квадрат суммы и сумма квадратов)
Не знаю, как учили Вас, но меня в школе учили запоминать эти ужасные формулы, учили даже несмотря на то, что на форзацах учебников (за разные классы) эти формулы были записаны.
А память это такая вещь, что сохраняет не всё и со временем всё забывается.
Но у человека есть другое свойство. То, что он понимает, он не забудет никогда.
Так и с этими формулами. Стоит только понять, о чем идет речь, так сразу и выясняется, что запоминать-то ничего и не надо было.
Итак, первая формула, по мне так основная. Квадрат суммы.
Если это сумма, то что-то должно складываться. Пусть это будут некоторые числа a и b. И пусть это будут длины отрезков, сумма которых образует сторону некоторого прямоугольника, квадрата, ведь стороны равны и угол между ними 90 градусов.
Общая длина стороны этого квадрата равна a+b. Это ведь сумма? Несомненно. А нам нужен квадрат суммы a+b. Возведем (a+b) во вторую степень. Кстати, а как найти площадь квадрата? Ну наверное также как и найти площадь любого прямоугольника, путем перемножения длины одной стороны на другую. Но у квадрата все стороны равны, значит надо сторону перемножить саму на себя. А перемножение числа самого на себя, это и есть возведение во вторую степень, в просторечии в «квадрат», поскольку данные рассуждения верны при поиске площади квадрата. Кстати, для нахождения объема куба будут аналогичные рассуждения, и как следствие перемножение стороны куба самой на себя, но уже трижды. Т.е. возведение числа в «куб».
Для других степеней «персональных» названий просто нет, т.к. пространство трехмерно (квадрат имеет два измерения, длину и ширину, куб кроме этого имеет еще и высоту).
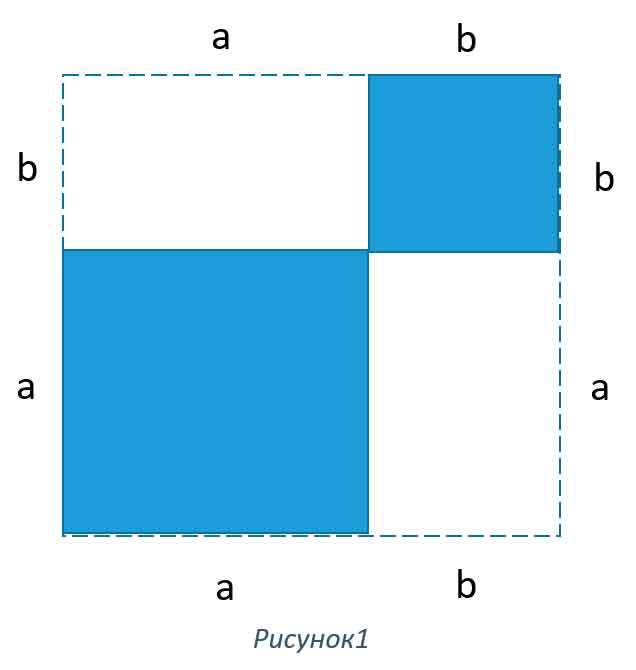
Ну и будем иметь дело с квадратами. Расположим два разных квадрата, (один со стороной a, второй со стороной b (квадраты синего цвета)), таким образом (Рисунок 1). Впишем эти два квадрата в третий (тот который пунктиром) у которого сторона равна (a+b). Найдем его площадь.
Это же просто. Длину стороны умножаем саму на себя. (a+b)(a+b) с одной стороны это (a+b)2 а с другой стороны это площадь нашего квадрата (см. Рисунок 1)
Избавимся от скобок.
(a+b)2 =(a+b)(a+b)=a2+2ab+b2
Как видим, можно было посчитать площадь квадрата со стороной (a+b) и чисто визуально. a2 это площадь одного синего квадрата, b2 это площадь второго синего квадрата, а 2ab это площадь двух не закрашенных прямоугольников. Сумма всех этих площадей и есть площадь квадрата со стороной (a+b).
Вот и получилась первая знакомая формула сокращенного умножения (a+b)2=a2+2ab+b2 – площадь квадрата со стороной (a+b)
К слову говоря вторая формула (сумма квадратов) тоже уже готова. Речь идет о квадратах со сторонами a и b (см. Рисунок 1). Нам ведь нужно узнать сумму площадей закрашенных квадратов, а для этого надо от общей площади квадрата со сторонами a+b вычесть площадь не закрашенных прямоугольников, а это будет (a+b)(a+b)-2ab=a2+2ab+b2-2ab
Ну и поменяем стороны равенства местами, чтобы формула суммы квадратов приняла более привычный нам вид
a2+b2=(a+b)(a+b)-2ab
Ну а разность квадратов и квадрат разности попробуйте вывести сами (Рисунок 2).
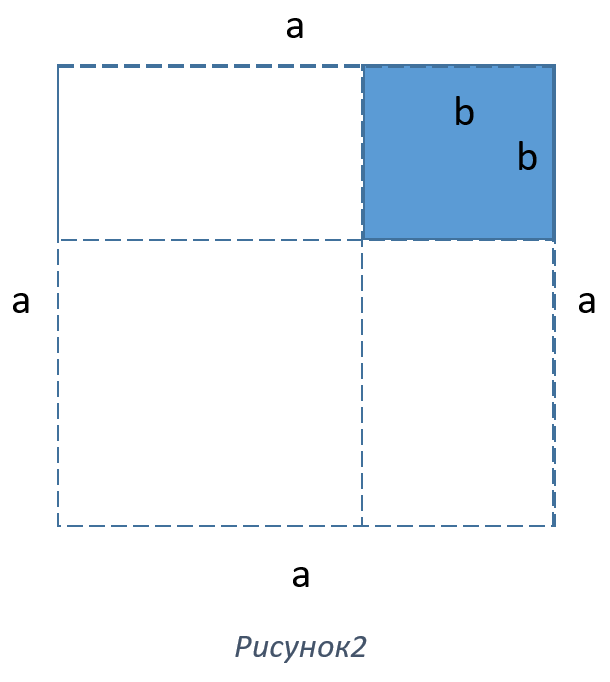
Должно получиться
a2-b2=(a-b)(a+b)
(a-b)2 =a2-2ab+b2
