В заметке «Пониматика (1). Формулы сокращенного умножения» я упомянул то, что по моему мнению понимание формулы «квадрат суммы» является отправной точкой для вывода целого ряда формул и теорем. Так, например, одно из доказательств «Теоремы Пифагора» (а их более 400 существует) прям-таки вытекает из «Квадрата суммы».
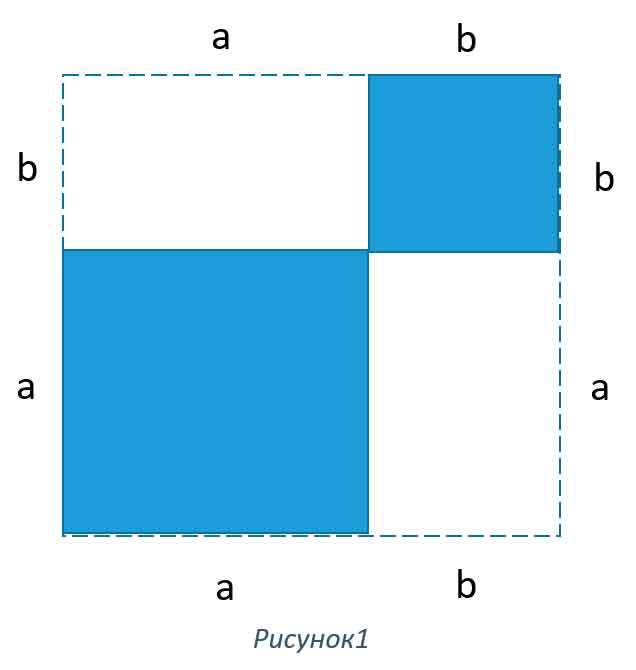
Рисунок 1 это как раз рисунок из заметки «Пониматика (1). Формулы сокращенного умножения.». Так-что просто продолжим рассуждения. Разделим один из прямоугольников пополам, проведя диагональ как показано на рисунке. Получим два прямоугольных треугольника у которых известны катеты и не известны гипотенузы, казалось бы, a2+b2=c2, так ведь нельзя так считать мы еще это только сейчас доказывать будем. Так-что гипотенуза c, нам пока не известна.
Достроим еще один квадрат, путем поворотов на 90o и отражений (поворотов на 180o), используя один из треугольников (любой, они же одинаковые) полученных из «разделения прямоугольника» (Рисунок 2)
Получается большой квадрат с полым квадратом (квадратным отверстием) со стороной c внутри, длина которой единственная неизвестна.
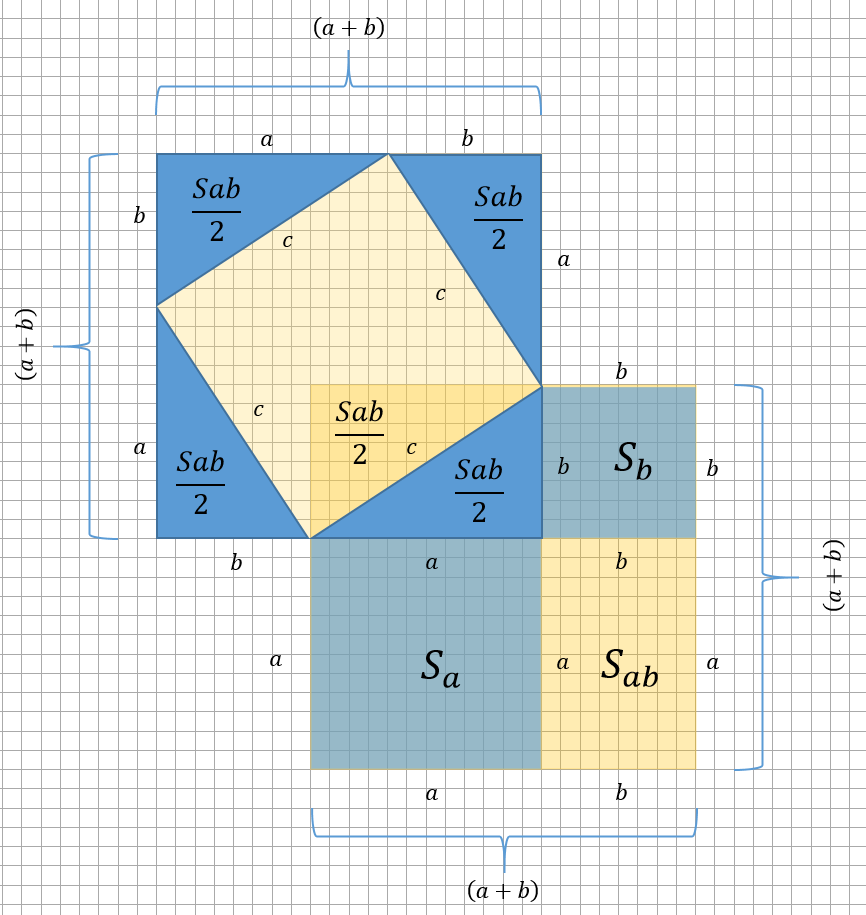
Зато известно все остальное (Рисунок 3).
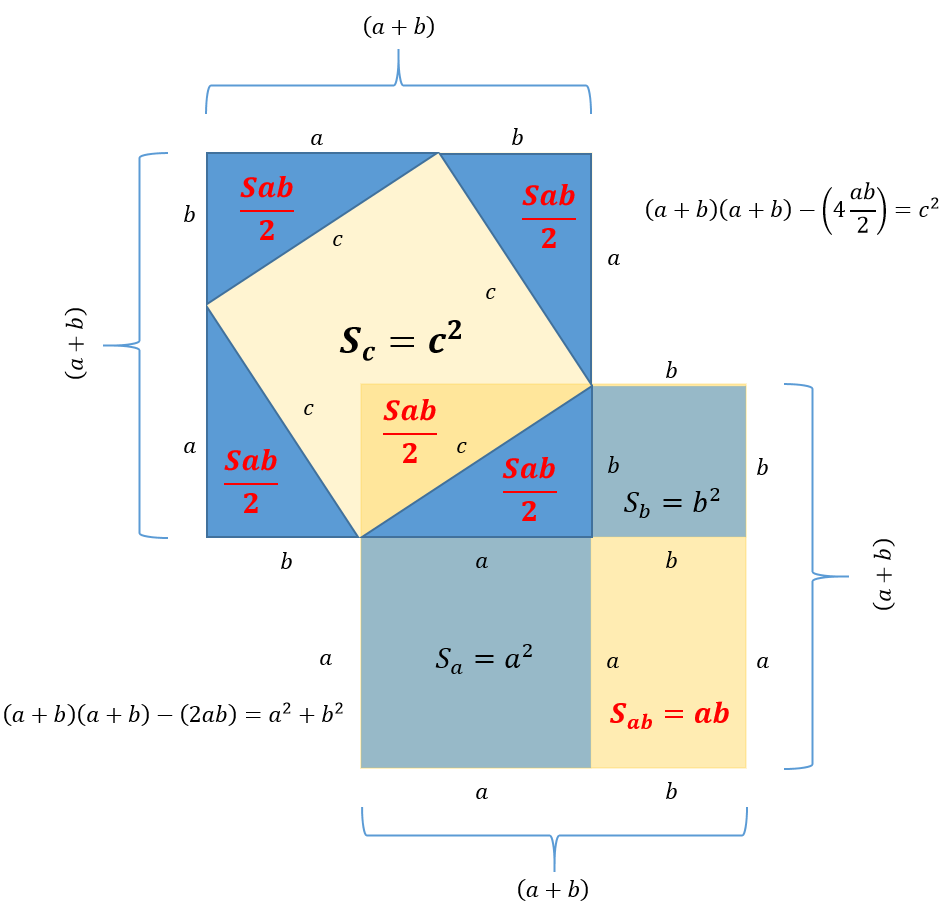
Нижний квадрат из формулы «Квадрата суммы» из которого вытекает формула «сумма квадратов» и верхний квадрат из которого, путем вычитания площадей треугольников из общей площади «Квадрата суммы» получается площадь квадрата со стороной c .
Вот и получилось что сумма площадей квадрата со стороной a и квадрата со стороной b равна площади квадрата со стороной c . Что и требовалось доказать.
a2+b2=c2
Вот теперь мы можем использовать (теперь уже с пониманием) в расчетах, то что сумма квадрата катетов равна квадрату гипотенузы
